Yesterday I gave my 9-year-old a bad math task.

I actually knew it was a bad math task, or at least a bad math task for her. It was the most unsurprising thing in the world when it failed, but I still gave it to her.

In my math classes for elementary teachers, some of my favorite moments are when we deconstruct a piece of math that went wrong. I especially love it when students begin to volunteer wrong answers: “I tried this, and I don’t know why it didn’t work,” or “I think this is wrong, but I want to know why it’s wrong.” We learn so much from these mistakes and wrong turns, and I think the same is true of teaching. I learn when I do something that works, but often I learn a lot more when I do something that doesn’t work. So in that spirit, I’m going to share the thing I did with my own child that didn’t work.

My goal was to help her expand her set of strategies for mental arithmetic. She has excellent strategies, by the way (I love sharing them with my students), but there are still times she labors over a calculation when I think there’s probably a more efficient method within her reach. Maybe, I thought, with a little help she could reach those methods.

So. The task. I decided to see if I could teach her a round-to-10-and-adjust strategy. That is, we can take away 9 by first taking away 10, and then adding 1. I threw together a Desmos activity, because kids like computers. (In retrospect, I think I already sensed that I was heading for failure, and I thought, technology! THAT will make her want to do this!) I did not spend very long making the task, which I offer not as an excuse, but…well, okay, maybe I am offering it as an excuse. Here it is, if you want to see it. If you don’t, here’s what you would see if you clicked on the link:

• A page guiding her through the strategy with the problem 13 – 9
• A page where she could draw the strategy on the number line
• A page where she could practice the strategy with other “subtract 9” problems
• Two pages extending the strategy (what if we subtract 8? what about 11?)
• A page of mixed practice

Again, I knew that this was not going to go well. But also, sometimes my students know that a strategy for solving a math problem isn’t going to work and they do it anyway. I think anyone in a problem-solving situation (mathematicians, teachers, parents, or basically anyone) sometimes knows something isn’t going to work, and yet does it anyway, not (always) because we’re irrational, but because trying a bad strategy can still provide us with good information.

I gave the task to my daughter, and as I watched my bad math task land with the thud it deserved, what I found most interesting was not that it didn’t work, but how it didn’t work.

What Went Wrong

The first indication that the task was going to flop came with the first sentence in the activity:

“Oh, it’s 4!” she said almost immediately, definitely not using her fingers.

“How did you do that?” I asked, and she explained her strategy (she knew 13 was 3 away from 10, and 9 was 1 away from 10, so she put together the 3 and the 1), but the point is not her strategy. The point is that:

Problem 1: My task was going to offer her a strategy she didn’t need.

She already knew how to solve 13 – 9, almost without thinking. She didn’t need me to tell her how to solve it.

Still, I pressed on. “Well, let’s continue and see another way you could solve the problem.” She willingly clicked on the buttons on the page that guided her through the subtract-10-then-add-1 strategy, and at the end she nodded. “That makes sense.”

I actually had expected that maybe it wouldn’t make sense to her. Encouraged, I moved on to the next slide, where she got to draw how the strategy worked on the number line. The picture she drew gave me the next indication that the task was not working:

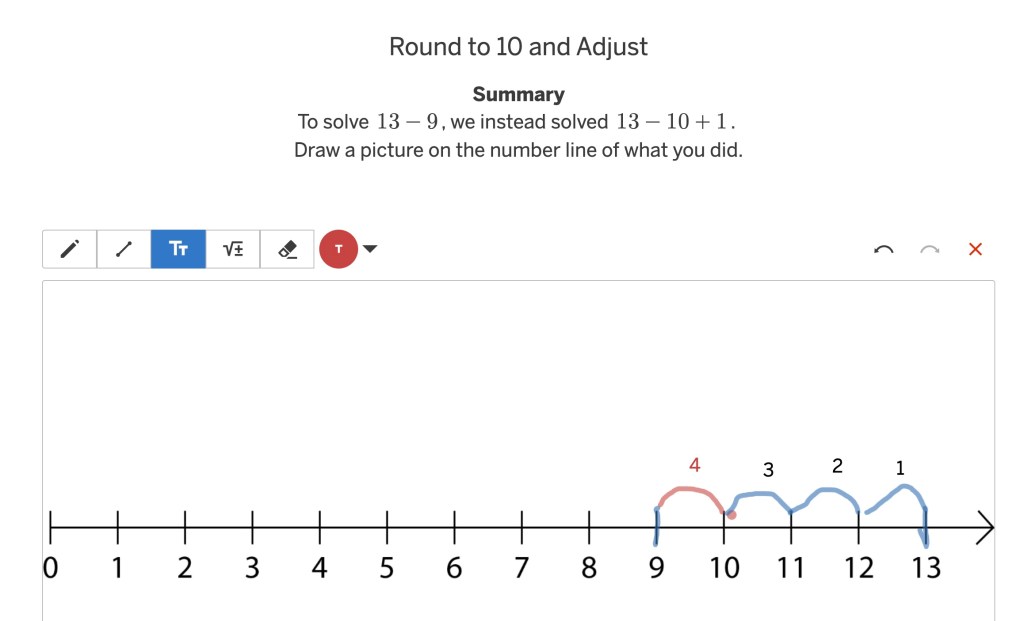
This was a perfect drawing of why 13 – 9 i s the same as 3 + 1. It just wasn’t the way that I was thinking about why 13 – 9 is the same as 3 + 1. I had designed the task around a take-away perspective (13 take away 9); Anya was thinking of subtraction from a difference perspective (the difference between 9 and 13). There was a mismatch between how she was thinking about the problem, and how my task “wanted” her to think about the problem.

Problem 2: There was no reason inherent to the task for her to engage with the intended learning goal.

With her strategy working out just fine for her, she zoomed through most of the next screen of practice problems. Then she got to the last problem on the screen, 25 – 9. Without hesitating, she wrote 26, then looked at me for approval.

“Great!” I said. “You got them all right except for that one.” I pointed to the last problem.

She stared at it for a moment, then deleted her answer and wrote 15.

“Um,” I said.

“14?” she asked. “13?” She started laughing. We both started laughing. She was totally just guessing now.

“Do you remember the strategy?” I asked, trying to salvage the task.

“Oh,” she said, and wrote 14.

“Remember? Subtract 10 and add 1?”

“That’s what I did,” she said. “Subtract 10 is 15. Then add 1.”

It wasn’t that she hadn’t learned the new strategy at all. It was that, while her strategy made sense to her, mine was just a set of steps. When her strategy was challenged by a harder problem, instead of thinking it through, she just tried to do what (she thought) I’d told her to do: subtract 10 (25 – 10 is 15), add 1 (which she interpreted as “subtract one more”).

Problem 3: Handing her a strategy without building understanding encouraged her to let go of her own number sense.

I think the fact that she ultimately landed on 14 was quite telling, because it was so obviously just following steps. She subtracted 10 (25 – 10 is 15), and then “added” 1 more to the amount she was subtracting (take away 1 more is 14). She was following the steps to the letter, but without understanding the intent it was a bit like a game of telephone where the message evolves as it passes from one person to the next.

And I think all of these together imply what was at the root of why the task just did not work:

My task failed to build on what she brought to the table.

I think I could find a better way. Will I? I don’t know. It’s summer break, and getting to do more math with my kids is one of the things I love about the summer, but there are lots of other things we do with our time, and teaching this particular strategy is more a curiosity than a priority for me. Helping her have good experiences with math is much more important than learning and using a particular strategy. But I do think considering what went wrong is worthwhile as I work on preparing lessons for the upcoming semester, and I hope that sharing might be worthwhile to someone else.

If you have a story of a failed task or lesson or teaching moment, in the classroom or with your own kids, I’d be interested in hearing it as well.

My daughter, a third grader, recently told me a story about a fractions task that was challenging for the kids in her class: How can you split a square into thirds?

To me, the task of dividing a square into thirds seems quite simple. This is how I would do it:

So when my daughter told me that the task was hard for her 3rd grade class, I had to step back from the immediate, easy mental image that came to my own mind and try to imagine what this task might look and feel like to a third grader. 

That’s challenging. I have few, if any, memories of my own experience with math as a third grader. But I am aware of a similar task that seems to be equally challenging for adults: How can you split an equilateral triangle into fourths?

When I give this problem to my college students, it stumps many of them completely, and there are few students who see it immediately. The ah-ha moments come slowly, but they do come, and eventually most students will produce something like this on their paper:

What I find most insightful about this task, though, is what students try that doesn’t work, and a correct solution that students almost never try:

What students try that doesn’t work:	What students almost never try:

Here’s my interpretation of this. First, students have a relatively stable understanding of fourths as “half, and then half again”. The most common version of this is to cut a shape in half vertically and horizontally (the “plus sign” version of a fourth). Second, students have an image of fractions as being composed of congruent pieces, or pieces that are the same size and shape. When students produce a “half, and then half again” image like the two above, it looks wrong to them. They don’t say, “Look, I did it!” They say, “I don’t think this works,” or, “Is this right?” When they come up with the congruent triangle version, they immediately know it works because it fits with their mental image of equal parts.

But the image on the right, the one they don’t come up with, also looks wrong to them, even though it’s not. The four pieces have exactly the same area (which you can easily prove if you understand that the all four triangles have the same height and base length), but they don’t all look the same. They are not congruent—they are the same size, but not the same shape.

In other words, their mental image of fourths and fractions gets in the way of completing the task.

I think something similar is going on with the third grade square task. First, just like adults have lots of mental images of fourths, but not fourths of triangles, I think kids have plenty of experience with thirds, but not thirds of squares. They see thirds of circles, of course, and even thirds of oblong rectangles, and while you’d think the leap from rectangle to square would be easy (a square is, after all, a type of rectangle), it’s not, and that may be partly because of the second point: Kids have lots of experience cutting squares into halves and fourths, and there’s just no way to halve your way to thirds.

Thirds look like this:	Fractions of squares look like this:

Imagining a square cut into thirds requires as much imagination for a third grader as is required for an adult to imagine a triangle cut into fourths.

Here was my daughter’s solution:

She thought it was quite a creative solution, and she was proud of it. But when you just see it drawn on paper, it’s probably hard to tell if it’s a correct solution. In fact, if you’re expecting this:

my daughter’s solution almost certainly looks wrong. So teachers (and parents) need creativity and imagination, too, as well as good questioning and listening skills.

Here’s how my daughter described her solution: “First I drew a line to cut the square in half, but I stopped it part of the way down—more than halfway, but not all the way. Then I drew a line straight across, where I stopped the first line, so there was a rectangle at the bottom of the square and two rectangles at the top. And if you took the rectangle at the bottom of the square and cut it in half and put one half on top of the other, you would get one of the rectangles at the top of the square.”

What you see in her picture is that thirds require three pieces. But what you hear in her description is that she also understands that the pieces must all be the same size, and that she can justify how her intended image does indeed meet that requirement by deconstructing and rearranging the pieces to show that all three are all the same size, even if they’re not congruent.

One of the things I love most about mathematics, and about teaching mathematics, is how both give me the opportunity to expand my imagination, but imagination is so foreign to many of my students’ experiences with school mathematics. Do you have your own examples of mathematical problems or concepts where imagination plays a role? I’d love to hear your ideas in the comments.

My 8-year-old was talking about doing some math this summer. “But interesting math,” he added.

“What’s something that’s not interesting math?” I asked.

“You know, like, 1 + 1. That’s not interesting.”

Well, he’d thrown down the gauntlet. So I got a piece of paper and wrote: 1 + 1 = 10. “True statement,” I told him, and then I introduced him to binary and he was engrossed in translating numbers to and from binary for the next half hour. 

Binary was the first thing that came to my mind, but binary isn’t the only way to make 1 + 1 interesting, and I have many more ideas where that came from.

On Wednesday we hiked to Corona Arch, just outside of Moab, Utah. The trail cuts across red rocks, too sturdy for human feet to cut a clear path, so much of the trail is marked with faded blue paint strokes every few yards. As we followed along, my 6-year-old said, “I’m counting the blue marks, but without numbers.”

“That’s impossible,” her older brother retorted. “You can’t count without numbers.”

“Yes I can,” she insisted.

“Are you noticing each mark?” I asked.

She agreed that this was what she was doing.

“But that’s not counting,” my son pressed.

“It’s like the ‘fish, fish, fish’ sketch from Sesame Street,” my husband said, and he was exactly right. In the “123 Count With Me” Sesame Street sketch (brilliantly commented on by Steven Strogatz in the New York Times), a furry monster tries to communicate a certain number of fish to Ernie as “fish, fish, fish, fish, fish, fish,” whereupon Ernie explains that a better way to communicate the quantity is with the number “six.” 

So when my daughter said she was “counting without numbers’, she was fish-fish-fishing the blue marks – noting each one, without assigning a number word. I knew what she was doing. But the dispute was about what to call what she was doing. Certainly she was engaging in a component of the counting process. I teach my college students that successful counting involves a one-to-one correspondence between words and counted objects, a consistent ordering of counting words, and a recognition that the last number said is how many there are. On the surface, she was just doing the first of these.

But I want to go deeper here, because the next thing that happened was that my son started wondering about how to say a number in binary, something that had come up the other day. In base ten, we group numbers by tens. As we count, we begin with “1, 2, 3, 4, 5, 6, 7, 8, 9”, but then instead of inventing a new number for one more than 9, we write 10, which means 1 ten and 0 ones. This means we can count as high as we want without continuing to invent new numbers to place in the sequence.

We don’t have to use ten, though. Various languages and writing systems have used 5, or 20, or even 60 for grouping. Binary uses 2. 1 is followed by 10, which doesn’t mean ten but rather 1 two and 0 ones. This is followed by 11 (1 two and 1 one), then 100 (1 group of two twos, or 1 four), and so on. If you count in binary, it’s still counting. 

But juxtaposing the counting without numbers discussion with the binary discussion made me wonder: what if we go still further and just count by ones? What if we called 1 thing “one”, 2 things “one one”, 3 things “one one one”, 4 things “one one one one”, and so on? Is this base one? And wouldn’t this still be counting in a sense? It’s like a tally. If I keep track of points in a game with a series of hash marks, I’m still counting points, aren’t I? If Ernie can ask, “How many fish?” and the monster can respond, “fish, fish, fish, fish, fish, fish”, and Ernie can provide him with the correct number of fish, haven’t the fish been counted? 

Granted, if you asked my daughter how many blue marks there were, she would not have been able to respond “mark, mark, mark…” with the correct number of marks. I don’t think what she was doing could actually be defined as counting. Her “counting without numbers” was not actually counting. And once I started asking my family if what she was doing was counting in base one, it became clear that I was the only one still interested in pursuing this line of thought. 

Still, I did find it intriguing that my daughter called what she was doing “counting without numbers.” Counting doesn’t stop being interesting once kids move out of preschool.

Not long ago my kindergartner was sitting at the counter finishing her breakfast toast when she pointed to two water bottles sitting in front of her. “Mama, is this math?” she asked. I tried to figure out what she was asking about. Were there number markings on one of the water bottles? I didn’t see any.

“Is what math?” I asked. 

“This,” she said, grabbing the yellow water bottle and moving it back and forth.

I stood up and walked over to see. She was looking intently at the water in the yellow bottle as it passed back and forth in front of the green one. As she did so, light shone through and turned the water in the yellow bottle green. 

“Oh,” I said, “how it changes the color?”

“Yes,” she confirmed. “Is that math?”

In retrospect I should have turned the question back to her: “Do you think it’s math?” or “Tell me why you think it might be math.” The question “What is mathematics?” is a really interesting and complicated question–we spend a whole semester talking about it in my college-level History and Philosophy of Mathematics course!

But sometimes daily life is distracting and I don’t think to ask the good questions until later. This time I just said, “Actually, what that looks like to me is science. Science and math do have a lot in common, though.” 

My second grader was listening in and he was not satisfied with my response. “But it kind of is math,” he piped up. “Because really, everything is math.”

I paused. “You’re right,” I said to him, and to my daughter. “There’s math in everything.” Because, even though I think it’s a bit more complicated than “everything is math”, so many of my college-age students tell me they never felt math was applicable to them, that math seemed unrelated to the questions that interested them. So I should want my kids to see math wherever they want to look for it, and be willing to look for it where they want to see it.

Yesterday I showed this picture to my kids and asked whether they thought there were more black ants or more red ants. Both of them immediately wanted to start counting the ants, but I stopped them because I was interested in how they thought about it without counting. 

My kindergarten-age daughter initially thought there were more red ants, because the arrangement looked “longer”, and indeed when she counted how many ants there were in a row, she found that the rows of red ants were longer and was satisfied that there were, indeed, more red ants. But when (with a little prompting) she counted the columns, she seemed surprised to count a longer line of black ants. She seemed more delighted than puzzled at this outcome, and was perfectly content to leave the question unresolved.

My 2nd-grade son decided pretty quickly that there were the same amount. He had seen his sister count the rows and columns, and in response to the puzzle of the different outcomes, he said, “You have to figure out how many are inside.” He then proceeded to count all the ants around the perimeter, and found 24 in both cases. “So since there’s the same amount all around,” he told me, “you know there will be the same amount inside.”

And then it was bedtime, and so I left it at that, with my daughter not knowing the answer and feeling interested but not overly invested in the question, and my son feeling quite confident in his incorrect, but very reasonable, solution. 

The fact that the conversation was interrupted gave me more time than usual to think about what happens next. Do I…

• Have them count the number of ants to see that there are actually 49 black ants and 48 red ants?
• Explore similar problems, with different numbers of ants?
• Manipulate the original pictures to help them  visually see the difference between black ants and red ants?
• See if they can create configurations of ants that push up against their initial theories?

When confronted with a “how would you respond?” question, my college students often ask, “But what is the right way to respond?” or “What is the best way to respond?” This is a hard question to answer! There are often some good ways and some not so good ways that you could respond (and sometimes a “good” way can backfire, and occasionally a “not so good” way can turn up something surprising). I don’t know that you can know the right way to respond, and sometimes you’ll experiment and it won’t go so well and then there’s always a next time.

I haven’t decided yet what direction to take (I’ve gotten lots of great ideas from folks on Twitter), but while whatever I do may or may not be “right”, I do have some general principles. I want to work with the thinking they’ve already given me rather than impose my own thinking on them. I want to spark their curiosity. I want to be flexible enough to go a different direction if that’s where their interest takes them. And I want whatever I do to happen in an environment of love and care.

I had a small math interaction with my kindergartener yesterday while we were doing some much-needed toy decluttering. We have a collection of toy cars that she plays with occasionally, but not often enough that it makes sense to keep all of them, so I told her she could keep ten. She pulled out a handful of favorites and counted: “One, two, three.” Then she added a couple more to the pile and counted them all again: “One, two, three, four, five.” Then two more: “One, two, three, four, five, six, seven.”

“Wait,” I said, seeing an opportunity. “You have seven already, and you get to keep ten. How many more can you choose?”

“I wish you hadn’t of asked me that!” she said, with a big sigh of 5-year-old exasperation. But she took up the problem. She began holding fingers up one at a time while quietly counting them, but stopped after a moment and just held up all the fingers on one hand and two fingers on the other. Then she looked at her hands and said, “Three!”

“Great!” I said. “Go ahead and choose three more cars that you want to keep.” 

“Do you know what I did?” she asked, before she started picking up the cars. “I looked at my fingers and I saw that I had three fingers down and I knew that’s what I needed.”

This was a brief interaction…but there was so much in that interaction for me to see! 

If you spend any time in the math education world these days, you’ll probably come across the questions What do you notice? and What do you wonder? The questions, when used well, can turn a mathematical activity from a teacher-driven activity to a student-driven activity, by stirring up and amplifying students’ inherent curiosity.

But these terms, notice and wonder, are also helpful in thinking about how we as parents or caregivers interact with children around their mathematical thinking. Instead of trying too hard to direct their mathematical learning, we often do more good by developing our own curiosity about their mathematical thinking, and our ability to simply notice what is happening in a given interaction.

Here are some of the things I noticed as I watched my daughter solve this problem: 

I noticed that she was smiling when she said, “I wish you hadn’t of asked me that!” Her big performative sigh told me that she knew I was asking her to do something she considered harder than simply counting the cars over and over until she reached ten. But this is a child who will not do something that she doesn’t want or have to do, and the smile told me she was up for the challenge.

I noticed that she didn’t count out all seven fingers. She started to, but quickly realized that she could just hold up five and two. This is a new development. She’s been counting on her fingers enough now that she is beginning to know what seven looks and feels like. Seven is more than just a count that ends at seven. It is also a relationship: a five and a two. 

I noticed that she also didn’t count the three or the ten. Once she had seven fingers up, she could see everything she needed to solve the problem: seven fingers up, three down, and ten in all. This is another relationship: seven fingers up and three down forms a ten. But also, she didn’t have to model all the actions of the story. She could look at a static image of seven and three and ten and relate it to a story with a beginning (cars she’s already chosen), middle (cars she still needs to choose), and end (all the cars she gets to keep).

I noticed that she explained her thinking unprompted. I almost always ask my kids, “How did you think about that?” and my husband does this, too. It’s just something we do in our household. So it wasn’t the explaining that was noteworthy here, but rather the fact that when I didn’t ask her (because my adult brain was already moving back the goal of decluttering the play space), she launched into an explanation anyway. It’s no longer just a parent-driven part of a math interaction–she now expects and wants to share her thinking.

One of the best things we can do to lay the groundwork for a love of mathematics is to notice what our children are thinking and seeing and doing (not just what we want them to think or see or do), to wonder with them, and to truly experience the wonder of watching them. When we approach our mathematical interactions with children with genuine curiosity, we see more, and children see that we see them.

Our family is lucky to live in a small city with great playgrounds. There are at least ten playgrounds in less than 20 square miles, which means that no matter where you live within the city, you’re likely within walking distance of one of them. They’re good playgrounds, too. Each is a little unique, most of them have been updated within the past few years, and all of them are surrounded by a good amount of open, grassy space for running around. As a parent of young children, this is one of the things I like best about where I live.

I wasn’t initially thinking about playgrounds when I first sat down to write this particular blog post. I went through several drafts before I got here. What I wanted to write about initially (and still do) was calculators, and how you should give your kid a calculator, earlier than you think you should give your kid a calculator, just to see what they do with it.

I got this idea from another parent, who had found that a calculator was the perfect toy to keep her kindergartener occupied during hour-long church services. So when my oldest was four, I went out and bought a cheap, solar-powered calculator and handed it to him just to see what he would do with it, and he loved it. A couple weeks ago at the start of the holiday break we were cleaning the house from top to bottom and came across the dusty calculator, languishing underneath a piece of furniture, and my now-7-year-old cried out, “My calculator! I love this!” and immediately jumped back into playing with it. 

Calculators sometimes get a bad rap, partly because most of us adults grew up in math classrooms where we were discouraged from using calculators except in carefully monitored situations. Then we all grew into a world where we basically have a calculator within arms reach 24 hours a day, 7 days a week, and it’s a tool we all use, but that we’ve nevertheless been conditioned to think of as sort of a cheat.

But to my child, the calculator is not a cheat or a shortcut, but a playground. No one has told him how it should or shouldn’t be used, and he can play with it and learn things about numbers and relationships that go well beyond his current numerical reasoning ability. He doesn’t play with it constantly, but each time he rediscovers it, his calculator play has changed a little to reflect his growing mathematical knowledge. His favorite calculator game when he was four was to enter in a randomish string of digits, like 827518271, and ask me to name the number. But now at age 7 he’s doing things like noticing that 8 ✕ 10 and 10 ✕ 8 give the same answer, wondering what other operations this works for, and stumbling across negative numbers when he tries it out on subtraction. A lot of this exploration is certainly stuff he might be able to do without a calculator, but the calculator removes the tedium of hand calculation and allows him to jump straight to the big questions.

I’ve been thinking a lot about playgrounds in my own classes of college students. Years ago when I was a beginning teacher, I would create “explorations” that were really just carefully guided activities where I had a series of pre-planned discoveries I intended my students to make. Unfortunately, I often found that my students could answer every question correctly without ever truly discovering the thing I’d been excited for them to discover. I found that my students were missing out on the wonder and delight of mathematics when I laboriously pre-arranged what they were going to wonder about and delight in.

I don’t think it’s wrong to have a sense of where you want students to end up, and while I’m constantly learning, I am nevertheless a much better lesson writer now than I was twenty years ago. But more and more I’ve been thinking about what it would mean to create and make room for true mathematical playgrounds in my instruction, spaces there’s the bare minimum structure and students can pursue the ideas that spark their curiosity. This is a hard vision for me to realize in practice. College students (most adults, really) often struggle with completely open exploration, and with knowing how to access the curiosity needed to explore. But kids come at this curiosity quite naturally, and don’t feel any compulsion to make their play look productive to an adult.

I wrote a guest post at Everywhere Math a little while ago where I talked about following your child’s agenda rather than your own, and the best mathematical playgrounds give the child agency to follow their own agenda. That’s what I’ve loved about handing my son a calculator.

What makes a tool or a toy or a book or an app or a game a playground? I don’t know that I have a full answer, but here are some questions I thought of:

• Is there more than one way to use it? 
• Do kids have a say in how to use it?
• Can you create your own rules?
• When adults join in, are they playing with the child (as opposed to directing the child’s play)? 
• Is it possible to imagine uses for which it was never intended?

If the answer to these questions is yes, then it might be a playground, and the very last step is to put it into a child’s hand and see what they do with it.